EFECTO DOPPLER
Llamado asi por el austriaco Christian Andreas Doppler. es el aparente cambio de frecuencia de una onda producido por el movimiento relativo de la fuente respecto a su observador.
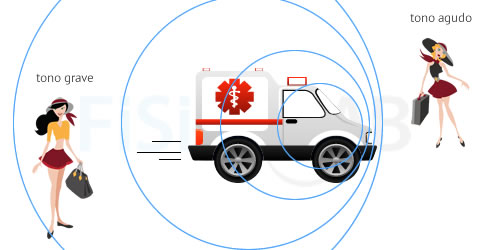
La ambulancia de la imagen se desplaza de izquierda a derecha. Cuando se acerca a la chica de la figura que lleva un maletín, en la derecha de la imagen, la onda "se comprime", es decir, la longitud de onda es corta, la frecuencia alta y, por tanto, el tono del sonido percibido será agudo. Por otro lado, cuando la ambulancia se aleja, a la izquierda de la imagen, la onda "se descomprime", es decir, la longitud de onda es larga, la frecuencia baja y, por tanto, el tono que percibe la chica que lleva el bolso será grave.
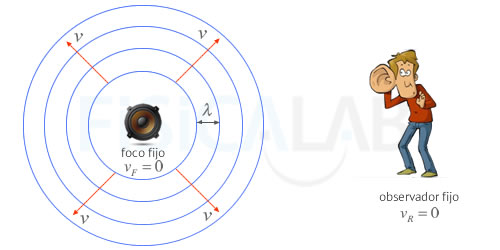
Foco y observador en reposo
Los círculos concéntricos de la figura representan los frentes de onda emitidos por el altavoz. A la derecha, un observador en reposo, percibirá la misma longitud de onda λ emitida por el foco.
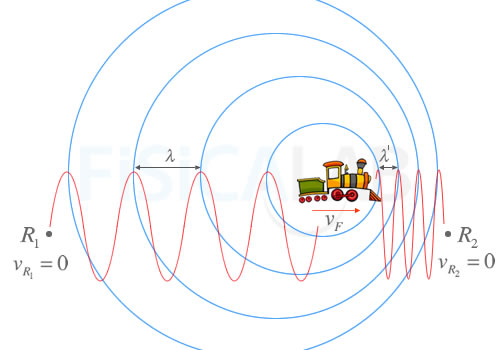
Foco en movimiento y observador en reposo
Frentes de onda generados por un foco en movimiento hacia la derecha. La frecuencia percibida por los receptores R1 y R2 será distinta, y dependerá de si el emisor se acerca o se aleja de ellos.
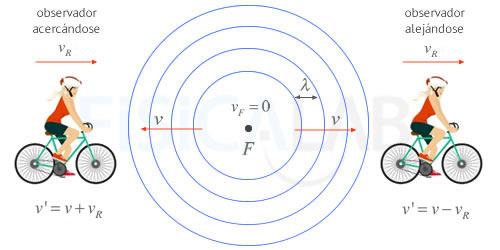
Foco en reposo y observador en movimiento
La separación entre dos frentes de onda permanece constante en todo momento. Aunque la velocidad de las ondas en el medio v también es constante, la velocidad relativa v' percibida por el observador que viaja a una velocidad vR depende de si este se aleja o se acerca al foco.
Imaginemos que un observador O se mueve hacia una fuente S que se encuentra en reposo. El medio es aire y se encuentra en reposo. El observador O comienza a desplazarse hacia la fuente con una velocidad . La fuente de sonido emite un sonido de velocidad , frecuencia f y longitud de onda . Por lo tanto, la velocidad de las ondas respecto del observador no será la v del aire, sino la siguiente:
. Sin embargo, no debemos olvidar que como el medio no cambia, la longitud de onda será la misma, por lo tanto si:
Pero como mencionamos en la primera explicación de este efecto, el observador al acercarse a la fuente oirá un sonido más agudo, esto implica que su frecuencia es mayor. A esta frecuencia mayor captada por el observador se la denomina frecuencia aparente y la simbolizaremos con f'.
El observador escuchará un sonido de mayor frecuencia debido a que
Analicemos el caso contrario:
Cuando el observador se aleje de la fuente, la velocidad v' será y de manera análoga podemos deducir que . En este caso la frecuencia aparente percibida por el observador será menor que la frecuencia real emitida por la fuente, lo que genera que el observador perciba un sonido de menor altura o más grave.
De estas dos situaciones concluimos que cuando un observador se mueve con respecto a una fuente en reposo, la frecuencia aparente percibida por el observador es:
Ahora consideraremos el caso donde el observador se encuentra en reposo y la fuente se mueve. Cuando la fuente se desplace hacia el observador, los frentes de onda estarán más cerca uno del otro. En consecuencia, el observador percibe sonidos con una menor longitud de onda. Esta diferencia de longitud de onda puede expresarse como:
Por tanto, la longitud de onda percibida será:
Como podemos deducir que:
Haciendo un razonamiento análogo para el caso contrario (fuente alajándose), podemos concluir que la frecuencia percibida por un observador en reposo con una fuente en movimiento será:
Cuando la fuente se acerque al observador se pondrá un (-) en el denominador, y cuando la fuente se aleje se lo reemplazará por un (+).
Al terminar de leer lo anteriormente expuesto surge la siguiente pregunta: ¿Qué pasará si la fuente y el observador se mueven al mismo tiempo?. En este caso particular se aplica la siguiente formula, que no es más que una combinación de las dos:
Los signos y deben ser respetados de la siguiente manera. Si en el numerador se suma, en el denominador debe restarse y viceversa.
Cuerdas
QUE ES UNA CUERDA VIBRANTE?
Es un cable elastico, tendido entre 2 puntos fijos, suceptible de emitir un sonido musical gracias a sus vibraciones.
Una tal cuerda , supuesta cilindrica y homogenea, puede vibrar longitudinalmente o transversalmente es alejada de su posicion de equilibrio. En musica utilizamos unicamente vibraciones tranversales.
Las cuerdas pueden ser hechas de acero (piano) o de tripa de obeja; se les aumenta el peso envolviendolas en helice con un alambre de cobre o de plata: obtenemos entonces cuerdas 'enfiladas' (notas graves del piano, sol del violin; cuarta cuerda).
Es un cable elastico, tendido entre 2 puntos fijos, suceptible de emitir un sonido musical gracias a sus vibraciones.
Una tal cuerda , supuesta cilindrica y homogenea, puede vibrar longitudinalmente o transversalmente es alejada de su posicion de equilibrio. En musica utilizamos unicamente vibraciones tranversales.
Las cuerdas pueden ser hechas de acero (piano) o de tripa de obeja; se les aumenta el peso envolviendolas en helice con un alambre de cobre o de plata: obtenemos entonces cuerdas 'enfiladas' (notas graves del piano, sol del violin; cuarta cuerda).

FORMULA DE LAS CUERDAS VIBRANTES
Una cuerda fijada a sus 2 extremidades presenta siempre un nudo de vibracion en sus extremidades y un cierto numero de nudos intermediarios. Ese sistema de ondas estacionarias se manifesta por un numero entero de zonas repartidas a lo largo de la cuerda. Si vemos k zonas, la longitud de cada zona es l / 2 , la longitud total de la cuerda L es dada por la expresion:
L = k *l / 2
g siendo la frecuencia y v la velocidad de ondas transversales. Obtenemos , puesto que l = v / g
L = k * v / 2*g
Pero v = Ö (F / m) d' où L = k /2g * Ö (F / m)
Ou encore g = k/2L * Ö (F / m)
g es en hertz (Hz o 1/s)
F es en newton (N)
L es en metros (m)
v es en metros por segundo (m/s)
k es un numero entero (k Î N)
m es la masa lineica de la cuerda, en gramos por metro (g/m)
Una cuerda fijada a sus 2 extremidades presenta siempre un nudo de vibracion en sus extremidades y un cierto numero de nudos intermediarios. Ese sistema de ondas estacionarias se manifesta por un numero entero de zonas repartidas a lo largo de la cuerda. Si vemos k zonas, la longitud de cada zona es l / 2 , la longitud total de la cuerda L es dada por la expresion:
L = k *l / 2
g siendo la frecuencia y v la velocidad de ondas transversales. Obtenemos , puesto que l = v / g
L = k * v / 2*g
Pero v = Ö (F / m) d' où L = k /2g * Ö (F / m)
Ou encore g = k/2L * Ö (F / m)
g es en hertz (Hz o 1/s)
F es en newton (N)
L es en metros (m)
v es en metros por segundo (m/s)
k es un numero entero (k Î N)
m es la masa lineica de la cuerda, en gramos por metro (g/m)
Tubos sonoros
Se llaman tubos sonoros aquellos que contienen una columna gaseosa (columna de aire) capaz de producir sonido al ser convenientemente excitada. El cuerpo sonoro es la columna gaseosa, y no el tubo que la contiene; en efecto, éste tiene la importante función de definir la forma de aquella pero fuera de esto, influye relativamente poco sobre los fenómenos sonoros. Los tubos sonoros pueden ser cerrados, es decir, que poseen una sola abertura y tubos abiertos, que poseen dos o más.
TUBOS CERRADOS
TUBOS ABIERTOS

| CLASIFICACIÓN DE LOS TUBOS SONOROS | ||||
|---|---|---|---|---|
Según el Modo de Excitación de la Columna de Aire
|
Tubos de Embocadura
|
Directa
| Flauta. Travesera,… | |
Indirecta
| Flauta. de pico, Tubos órgano,… | |||
Tubos de Lengüeta
|
Libres
| Arcordeón, Armónica,… | ||
Batientes
| Simples | Clte., Saxofon., Tubos órgano… | ||
| Dobles | Oboe, Fagot,… | |||
Tubos de lengüeta labial o membrana
|
Trompeta, Trompa, trombón, Tuba…
| |||
Según la obtención de la escala
|
Tubos con orificios
|
Instrumentos de Viento Madera,…
| ||
Tubos de longitud variable
|
Vara
| Trombón de varas | ||
Pistones
| Trompeta,… | |||
Válvulas Rotatorias
| Trompa, Tuba,… | |||
Según su Forma Interior
|
Cónicos
|
Saxofón, Fagot,…
| ||
Cilíndricos
|
Flauta travesera, Clarinete,…
| |||
Prismáticos
|
Instr. Primitivos, algunos tubos del órgano…
| |||
OPTICA
NATURALEZA DE LA LUZ
La luz emitida por las fuentes luminosas es capaz de viajar a través de materia o en ausencia de ella, aunque no todos los medios permiten que la luz se propague.
Desde este punto de vista, las diferentes sustancias materiales se pueden clasificar en opacas, traslúcidas y transparentes. Aunque la luz es incapaz de traspasar las opacas, puede atravesar las otras. Las sustancias transparentes tienen, además, la propiedad de que la luz sigue en su interior trayectorias definidas. Éste es el caso del agua, el vidrio o el aire. En cambio, en las traslúcidas la luz se dispersa, lo que da lugar a que a través de ellas no se puedan ver las imágenes con nitidez. El papel vegetal o el cristal esmerilado constituyen algunos ejemplos de objetos traslúcidos.
En un medio que además de ser transparente sea homogéneo, es decir, que mantenga propiedades idénticas en cualquier punto del mismo, la luz se propaga en línea recta. Esta característica, conocida desde la antigüedad, constituye una ley fundamental de la óptica geométrica.
Dado que la luz se propaga en línea recta, para estudiar los fenómenos ópticos de forma sencilla, se acude a algunas simplificaciones útiles. Así, las fuentes luminosas se consideran puntuales, esto es, como si estuvieran concentradas en un punto, del cual emergen rayos de luz o líneas rectas que representan las direcciones de propagación. Un conjunto de rayos que parten de una misma fuente se denomina haz. Cuando la fuente se encuentra muy alejada del punto de observación, a efectos prácticos, los haces se consideran formados por rayos paralelos. Si por el contrario la fuente está próxima la forma del haz es cónica.
COMPORTAMIENTO DE LA LUZ
Teoría Corpuscular (Isaac Newton)
Plantea que la luz esta compuesta por partículas que son emitidas por los cuerpos luminosos.
Observaciones:
a) La luz se propaga en linea recta
b) cuando se interpone un obstáculo, se produce la sombra
c) cuando los corpúsculos rebotan sobre una superficie se produce la reflexión.
b) cuando se interpone un obstáculo, se produce la sombra
c) cuando los corpúsculos rebotan sobre una superficie se produce la reflexión.
Lo que no podía explicar:
a) ¿Por que los cuerpos no pierden masa al emitir corpúsculos?
b) ¿Por que algunos corpúsculos se reflejan y otros se refractan?
a) ¿Por que los cuerpos no pierden masa al emitir corpúsculos?
b) ¿Por que algunos corpúsculos se reflejan y otros se refractan?
Teoría Ondulatoria (Christian Huygens)
Plantéa que la luz es una onda que necesita un medio material para propagarse, el que denominó éter.
Observaciones:
a) La masa de los cuerpos que emiten luz no disminuye
b) La propagación rectilinea y la reflexión se pueden explicar como una onda
c) La luz experimenta refracción, que es un fenómeno tipico de las ondas.
Fue Thomas Young (1773-1829) quien pudo observar la difracción e interferencia, fenómenos propios de las ondas y que la teoria no era capaz de explicar.
b) La propagación rectilinea y la reflexión se pueden explicar como una onda
c) La luz experimenta refracción, que es un fenómeno tipico de las ondas.
Fue Thomas Young (1773-1829) quien pudo observar la difracción e interferencia, fenómenos propios de las ondas y que la teoria no era capaz de explicar.
Lo que no podía explicar:
a) ¿Por que la luz se propaga en el vacío?
Teoría del comportamiento dual
Teoría del comportamiento dual
No fue hasta el siglo XX cuando se aceptó que la luz tiene ambos comportamientos, luz y onda, dependiendo del fenómeno observado.
Las ondas se difractan notoriamente mientras más parecida a la longitud de onda es la abertura por donde pasa. Para ver difracción en la luz se debe hacer un orificio muy pequeño, lo que sugiere que su longitud de onda es muy pequeña (micron). Por esta razón no observamos la difracción de la luz cuando entra por la ventana. El sonido en cambio tiene longitudes de onda mucho mayores (cm a m), y por ello se difracta al entrar por la ventana, una puerta, o una ranura cualquiera.
La velocidad de la luz. En el vacío es por definición una constante universal de valor 299.792.458 m/s(suele aproximarse a 3·108 m/s), o lo que es lo mismo 9,46·1015 m/año; la segunda cifra es la usada para definir al intervalo llamado año luz. Se simboliza con la letra c, proveniente del latín celéritās (en español celeridad o rapidez), y también es conocida como la constante de Einstein.[cita requerida] El valor de la velocidad de la luz en el vacío fue incluida oficialmente en el Sistema Internacional de Unidades como constante el 21 de octubre de 1983, pasando así el metro a ser una unidad derivada de esta constante. La rapidez a través de un medio que no sea el "vacío" depende de su permitividad eléctrica, de su permeabilidad magnética, y otras características electromagnéticas. En medios materiales, esta velocidad es inferior a "c" y queda codificada en el índice de refracción. En modificaciones del vacío más sutiles, como espacios curvos, efecto Casimir, poblaciones térmicas o presencia de campos externos, la velocidad de la luz depende de la densidad de energía de ese vacío
REFLEXION Y REFRACCION
Reflexión de la luz es el cambio de dirección que experimenta la luz cuando choca con un objeto y "rebota"
La reflexión de la luz hace posible que veamos objetos que no emiten luz propia.
Elementos de la reflexión
En la reflexión podemos señalar los siguientes elementos:
- Rayo incidente: Es el rayo de luz que incide en la superficie
- Rayo reflejado: Es el rayo que sale de la superficie
- Normal: es la línea imaginaria perpendicular a la superficie
- Ángulo de incidencia (i) es el ángulo que forman el rayo incidente y la normal
- Ángulo de reflexión (r) es el ángulo que forman la normal y el rayo reflejado.
Leyes de la reflexión
- Primera ley: El rayo incidente, el rayo reflejado y la normalestán en el mismo plano.
- Segunda ley: El ángulo de incidencia es igual al ángulo de reflexión.
Clases de reflexión
Según las superficies en que incidan los rayos luminosos, la reflexión puede ser especular o difusa.
- Reflexión especular: Cuando las superficies son pulidas, los rayos luminosos se reflejan en una sola dirección y de forma ordenada. Por ello se forman imágenes que parecen copias de los objetos.
- Reflexión difusa: Se produce cuando las superficies son irre- gulares. En este caso, los rayos luminosos se reflejan en todas direcciones, lo que no permite la formación de imágenes
La Refracción de la luz
Refracción de la luz es el cambio de dirección que sufre la luz cuando pasa de una sustancia transparente a otra. Ejemplo, el aire, a otro, como el agua.
Los rayos de luz que cambian de dirección se llaman rayos refractados.
Al introducir una cuchara en un vaso con agua parece que se dobla o se corta, porque los rayos de luz se desvían, ya que viajan más lento al pasar del aire, donde existen menos partículas, al agua, donde hay más.
Leyes de la refracción
- Primera ley: El rayo incidente, la normal y el refractado se encuentran en un mismo plano.
- Segunda ley: Si un rayo incidente pasa de un medio a otro de mayor densidad, el rayo refractado se acerca a la normal. Pero, si pasa a otro de menor densidad, el rayo refractado se aleja de la normal.
Elementos de la refracción
En toda refracción podemos distinguir los siguientes elementos:
- Rayo incidente: es el rayo que incide sobre la superficie de ambos medios en forma oblicua.
- Rayo refractado: es el rayo que atraviesa el medio y cambia su dirección y velocidad.
- Normal: es la línea imaginaria perpendicular a la superficie
- Ángulo de incidencia (i). Es el ángulo que forman el rayo incidente y la normal.
-Ángulo de refracción (r). Es el ángulo que forman la normal y el rayo refractado.
Espejos |
Los espejos son quizá el instrumento óptico más antiguo. Los egipcios de hace cuatro mil años emplearon metales pulidos para reflejar sus caras. Sin embargo, no fue sino hasta 1857 cuando se inventaron los espejos gracias a Jean Foucault , quien desarrolló un método para recubrir el vidrio con una capa de plata.
| a) Espejos planos |
Si una persona se mira en un espejo, como por ejemplo en el espejo del baño, apreciará su imagen en un espejo plano. Un espejo plano es una superficie plana y lisa que refleja la luz de manera regular. En el ejemplo, la persona que se mira es el objeto. Un objeto es una fuente de rayos divergentes de luz que puede ser luminoso como una vela o una lámpara o iluminado como la Luna o la página de un libro que esté leyendo. En el caso de un objeto iluminado, éste refleja la luz de manera difusa en todas direcciones.
La figura a la derecha muestra cómo algunos de los rayos inciden desde el punto P sobre el espejo y se reflejan con ángulos de incidencia y reflexión iguales (recordar que el ángulo de incidencia se forma cuando llega el rayo a la superficie y el de reflexión cuando se devuelve).
Luego de la reflexión, los rayos continúan dispersándose. Si se prolongan los rayos hacia atrás (líneas de visión), por la parte posterior del espejo, como se ve con las líneas discontinuas, se puede observar en el dibujo que se intersecan en el punto P'. El punto P', en donde los rayos prolongados aparentemente se intersecan, se llama imagen. Aun cuando para un observador, los rayos parecen venir del punto P', se observa que allí no existe fuente alguna. Por tal razón, esta imagen se denomina imagen virtual.
| b) Espejo cóncavo |
Si se examina la superficie interna de una cuchara se tiene un espejo cóncavo, el cual refleja la luz. Está conformado por un número muy grande de espejos planos pequeños montados sobre la superficie de una esfera.
| c) Espejo convexo |
Un espejo convexo es un objeto esférico que refleja luz desde la superficie externa. La parte externa de una cuchara es un ejemplo. Los rayos reflejados siempre divergen y, por tanto, no forman imágenes reales.
Los Lentes
Las lentes son objetos transparentes, usualmente de vidrio, limitados por dos superficies, de las que al menos una es curva. Las propiedades de las lentes se deben a la refracción de la luz que pasa a través de ellas.
Hay dos tipos de lentes, convergentes y divergentes. Los lentes convexos son convergentes, y los lentes cóncavos son divergentes. Tener en cuenta que los rayos de luz golpean la lente, ellos se curvarán hacia la parte más ancha. Esta es la razón por la que los lentes convexos son convergentes. Como los rayos de luz golpean la lente, ellos curvan hacia el centro, que es la parte más ancha, y los rayos de luz cruzarán entre ellos.
-Lentes convergentes
Los lentes convergentes son más gruesos por el centro que por los extremos, y concentran en un punto los rayos de luz que las atraviesan. A este punto de le denomina foco y la separación entre el y el lente se conoce como distancia focal.
Estos lentes se usan mucho en instrumentos ópticos y también para la corrección de la hipermetropía, ya que no ven bien de cerca y tienen que alejarse de los objetos.
-Lentes divergentes
Los lentes divergentes son mas delgados en la parte central que en los extremos, por lo cual también se les denomina cóncavos, y solo producen imágenes virtuales, es decir, una imagen más pequeña situada delante del objeto. En las gafas o anteojos para miopes, las lentes cóncavas hacen que los ojos formen una imagen nítida en la retina y no delante de ella.
El objetivo de este artículo es relacionar los diversos instrumentos ópticos así como sus mecanismos de convergencia – divergencia, entre otros. También establecer sus diversas funciones.
Para finalizar, hablaremos acerca de la visión que utiliza el sistema de los lentes, proveyendo ese don que es la vista
La lupa o microscopio simple
Lupa es el instrumento óptico de amplitud más simplificada que existe. Su principal uso es obtener imágenes ampliadas, de modo que sus menores detalles pueden ser observados con perfección.
La lupa, también llamada microscopio simple, consiste en una lente convergente, luego crea imágenes virtuales. En términos generales, cualquier lente de aumento puede ser considerada lupa. Hay tipos que poseen un soporte que contiene la lente, un armazón articulado donde se pone la lámina con el objeto a ser observado y un espejo convergente (condensador) para concentrar a los rayos luminosos sobre el objeto.
El objeto deberá ser ubicado a una distancia de la lente, menor que la distancia focal de ella. Existe una condición para que la imagen formada sea nítida. De acuerdo con el foco del objeto del lente usado como lupa, tendremos una distancia mínima para obtener una visión nítida. Si la lente es puesta próxima a un objeto a una distancia menor que a la distancia mínima de visión nítida, la imagen no será visible.
TELESCOPIO ASTRONÓMICO
Los telescopios astronómicos son instrumentos ópticos de acercamiento/aproximación, usadas en la observación de objetos muy alejados. Los telescopios astronómicos son formados por dos sistemas ópticos distintos: una lente objetiva de gran distancia focal que proporciona una imagen real e invertida del objeto observado, y una lente ocular con distancia focal menor que proporciona una imagen virtual e invertida del objeto.
Los dos sistemas son puestos en las extremidades opuestas de un conjunto de tubos concéntricos, que se encajan unos en los otros variando el largo del conjunto permitiendo focalizar mejor el objeto a ser observado. Los telescopios de grande porte y capacidad de amplitud poseen un telescopio más chico buscador, una vez que los primeros poseen determinado campo de visión.
La diferencia principal entre los telescopios astronómicos y terrestres es, no solamente el porte, sino también la posición de la imagen. Los astronómicos presentan la imagen final invertida, y las terrestres presentan la imagen en la posición real del objeto pues poseen un sistema de lentes adicionales entre las lentes objetiva y ocular.
MICROSCÓPIO COMPUESTO
El microscopio compuesto, o simplemente microscopio, es un instrumento usado para observar regiones minúsculas cuyos detalles no pueden ser visualizados a simple vista.
Es basado en el conjunto de dos lentes. La primera es la objetiva y fuertemente convergente (fornece una imagen real y invertida) y posee pequeña distancia focal, queda volteada para el objeto y forma en el interior del aparato la imagen del objeto.

La segunda lente es ocular y también posee pequeña distancia focal, es menos convergente que la objetiva, permite al observador ver esa misma imagen por formar una imagen final y directa.
Tales lentes son puestas diametralmente en extremidades opuestas de un tubo, formando lo que llamamos cañón. El sistema que permite el alejamiento o acercamiento del conjunto ocular – objetiva permite una mejor visualización del campo observado cuando lo focalizamos.
CÁMARA FOTOGRÁFICA
La cámara fotográfica tal cual instrumento óptico de proyección, se basa en el principio de que un objeto visualizado a través de una lente convergente, a una distancia mayor que la distancia de la misma, produce una imagen real e invertida, y más todavía: su tamaño es inversamente proporcional a la distancia foco – objeto. La lente o sistema de lentes empleada recibe el nombre de objetiva.
Es importante que la imagen sea proyectada sobre el film, pues si la imagen se proyecta antes ó después del film do filme tendremos una foto fuera de foco. Para eso ajustase las lentes objetivas para obtener una imagen nítida. Cuando en foco, la imagen formada en el film fotográfico es real e invertida.
MATEMÁTICAS
ÁREA BAJO UNA CURVA
La formulación del área bajo una curva es el primer paso para desarrollar el concepto de integral. El área bajo la curva formada por el trazo de la función f(x) y el eje x se puede obtener aproximadamente, dibujando rectángulos de anchura finita y altura f igual al valor de la función en el centro del intervalo.
Si hacemos mas pequeño la anchura del rectángulo, entonces el número N es mas grande y mejor la aproximación al valor del área.
INTEGRAL DEFINIDA
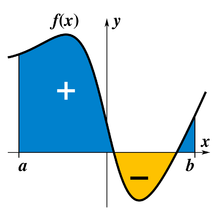
La integral definida de una función representa el área limitada por la gráfica de la función, en un sistema de coordenadas cartesianas con signo positivo cuando la función toma valores positivos y signo negativo cuando toma valores negativos.
CONSTANTE DE INTEGRACIÓN
El uso de la constante de integración es una manera de expresar el resultado general de una integral indefinida que surge en un problema físico. El proceso de integración no da un valor específico de la integral, pero la aplicación de las condiciones iniciales físicas, posibilita la asignación de un valor específico a la constante de integración, permitiendo de esta manera el cálculo para una situación física específica
REGLA DE LA CADENA PARA ANTIDERIVACION
FORMULAS DE INTEGRACIÓN

INTEGRALES TRIGONOMÉTRICAS
LOGARÍTMICAS
Integrales logaritmicas
Integrales exponenciales
Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x = a y x = b.
La integral definida se representa por  .
.
∫ es el signo de integración.
a límite inferior de la integración.
b límite superior de la integración.
f(x) es el integrando o función a integrar.
dx es diferencial de x, e indica cuál es la variable de la función que se integra.
DEFINICIÓN DE SUMATORIASi f es una funcion que asume valores tanto positivos como negativos sobre [a,b], entonces la integral definida :
no representa el area bajo la grafica de f sobre el intervalo.
El valor de:
Suponga que la funcion y = f(x) es continua sobre el intervalo [a,b] y que f (x) <0 sobre [a,c) y que f (x) >/ 0 sobre [c,b].
El area total es el area de la region acotada por las graficas de f, el eje x y las rectas verticales x=a y x=b.
Para encontrar el area se emplea el valor absoluto de la funcion y= | f(x) |, que no es negativa para toda en x en [a,b].
TEOREMA FUNDAMENTAL DEL CALCULO
El Teorema Fundamental del Cálculo proporciona un método abreviado para calcular integrales definidas, sin necesidad de tener que calcular los límites de las sumas de Riemann. Conceptualmente, dicho teorema unifica los estudios de la derivación e integración, mostrando que ambos procesos son mutuamente inversos.

VOLUMEN DE ROTACIÓN
En principio, cualquier cuerpo con simetría axial o cilíndrica es un sólido de revolución. Se denomina sólido de revolución o volumen de revolución, al sólido obtenido al rotar una región del plano alrededor de una recta ubicada en el mismo, las cuales pueden o no cruzarse. Dicha recta se denomina eje de revolución.


















No hay comentarios:
Publicar un comentario